Big Data
탐색적 분석 - 통계 분석
by jun_code
2022. 5. 20.
기술통계
- 수집된 데이터로부터 평균, 분산 등의 요약 통계량이나 그래프를 이용하여 정리 요약하여 전반적 특성을 파악하는 기술
기술통계
- 중심 척도 : 산술평균, 중위값, 최빈치
- 평균은 이상치에 영향을 받지만 중앙값은 이상치의 영향이 적음
- 산포 척도 : 분산, 표준편차, 범위
- 분포 모양 : 빈도, 상대도수, 비대칭도(왜도), 첨도
- 왜도 : 분포의 치우침 정도로 음수이면 오른쪽으로 치우침
- 첨도 : 분포의 뾰족한 정도로 양수이면 더 뾰족함
데이터 유형
- 연속형 데이터 : 연속적을 측정될 수 있는 것 => 사람이 셀 수 없는 것
- 등간 척도 : 같은 간격을 가지지만 절대 영점이 없는 척도 ex) 온도, 물가지수
- 비율 척도 : 비율의 개념이 추가되어 절대적 기준값이 존재하는 척도 ex) 중량, 강도
- 이산형 데이터 : 발생 빈도를 세어서 산출한 것 => 사람이 측정한 것
- 명목 척도 : 변수간 사칙연산은 의미가 없음 ex) 성별, 등번호
- 순위 척도 : 관찰대상이 가진 속성 크기에 따라 서열 부여 ex) 만족도, 등급
확률 분포
- 확률 : 경험이나 실험의 결과로 사건이나 결과가 발생할 가능성
- 확률 분포 : 확률 변수가 특정 값을 가질 확률(상대적 가능성)
- 분포
- 연속 확률 분포 : 정규분포, 표준정규분포, t분포, 카이제곱 분포, F 분포, 와이블 분포
- 이산 확률 분포 : 베르누이 분포, 이항분포, 포아송 분포, 초기하 분포
- 표본통계량
- 표본 평균 : 정규분포, t-분포
- 표본 분산 : 카이제곱 분포, F 분포
- 표본 비율 : 이항 분포
- 중심극한 정리
- 모집단으로부터 크기가 n인 확률표본을 취할 때, 확률표본의 분포는 크기 n이 큰 경우 정규분포를 따름
정규분포
- 평균을 중심으로 좌우 대칭의 종모양 분포
- 어떤 실수값이라도 모두 최할 수 있는 연속확률변수 X에 관한 분포

표준정규분포
- 정규분포 밀도함수를 통해 X를 Z로 정규화하여 평균이 0, 표준편차가 1인 표준정규분포
t분포
- 정규분포의 평균을 측정할 때 사용
- 모평균의 검추정에서 모표준편차를 모르는 경우에 정규분포 대신에 사용
- 0을 중심으로 좌우 대칭으로 더 평평하고 긴 꼬리를 가짐

카이제곱분포
- 정규분포를 따르는 모집단에서 크기가 n인 표본을 무작위로 반복하여 추출하였을 때, 각 표본에 대해 구한 표본 분산은 카이제곱 분포를 따름
- 모집단의 분산 추정 / 빈도기반의 분포 및 형태 적합도 검정 / 집단 간의 독립성 및 동질성 검정


F 분포
- 분산이 같은 두 정규모집단으로부터 확률표본을 반복하여 독립적으로 추출한 후, 두 표본분산의 비율들의 표본분포
- 두 분포의 분산 비교에 사용 / ANOVA에서 그룹 내 변동과 그룹 간 변동으로 여러 평균값을 비교하는데 활용
- 표준정규분포를 제곱하여 합한 카이제곱분포 2개를 서로 나눈 값으로 0보다 큰 영역에 위치함


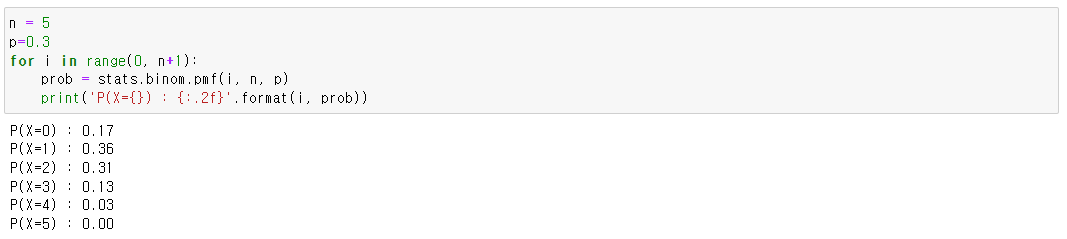
이항분포
- 베르누이 실험을 여러 번 시행해서 특정한 횟수의 성공/실패가 나타날 확률
- 베르누이 실험 : 시행 횟수가 1회인 경우(n=1)
추론 통계
- 표본에 포함된 정보로부터 모집단의 특성을 파악하고 타당성을 검토하여 모수를 추론하거나 미래를 예측하는 기술
통계적 추론
- 기술 통계 : 측정이나 실험을 통해 수집한 통계 자료의 정리/표현/요약/해석을 통하여 자료의 특성을 규명하는 방법과 기법
- 추론 통계 : 한 모집단에서 추출한 표본에 대해 그 모집단의 어떤 특성에 대해 결론을 추론하는 절차와 기법
추론 통계
- 정의 : 표본에 포함된 정보로부터 모집단의 특성을 파악하고 타당성을 검토하고 모수를 추론하거나 미래를 예측하는 것
- 통계적 추정 : 표본의 성격을 가지는 통계량을 기초로 하여 모수를 추정하는 통계적 분석 방법
- 가설 검정 : 모수에 대해 가설을 세우고, 표본을 선택하여 통계량을 계산한 다음에 이에 기초하여 가설의 진위 판단
- 모수 : 모집단의 기술적 척도
- 통계량 : 표본의 기술적 척도
추정
- 정의 : 모집단에서 추출한 표본에서 얻은 정보를 이용하여 모집단의 평균, 표준편차 등을 추측하는 것
- 종류
- 점 추정 : 추정하고자 하는 모수를 표본 데이터를 이용하여 하나의 수치로 추정함
- 구간 추정 : 추정하고자 하는 모수가 존재할 것으로 예상되는 구간을 정하여 추정
- 신뢰 수준 : 추정하고자 하는 모평균이 신뢰구간에 포함될 확률 ex) 95%, 99%
점추정
- 정의 : 표본 데이터를 이용해 계산된 하나의 숫자로 모수의 값을 추측하는 과정을 말함
- 추정 대상 : 모평균, 모표준편차, 모분산, 모비율
구간추정
- 정의 : 추정하고자 하는 모수가 존재할 것으로 예상되는 구간을 정하여 추정
정규성 검정
- 정의 : 확률분포가 정규분포를 따르는지 아닌지를 확인하는 것 => shapiro 사용
from scipy.stats import shapiro
- 귀무가설과 대립가설
- 귀무가설(H0) : 모집단은 정규분포를 따른다 (cf. 상관분석에서 상관이 없다, 회귀분석에서 β=0) => p-value가 0.05보다 크면 정규분포를 따른다
- 대립가설(H1) : 모집단은 정규분포를 따르지 않는다 (cf. 상관분석에서 상관이 있다, 회귀분석에서 β!=0)




모평균 신뢰구간 추정
모표준편차를 아는 경우 : 신뢰도 = 1-α


모표준편차를 모르는 경우 : 신뢰도 = 1-α

- 일반적으로 모수를 잘 모르기에 주로 표본에서 표준편차를 추정해야함
- 표본이 30개 이상이면 t분포가 정규분포와 비슷해 지기에 정규분포를 사용해도 됨

통계적 가설 검정
- 표본을 통해 얻은 정보를 이용해 모집단의 특성에 대한 가설의 진위를 판단하는 과정
- 절차
- 1. 가설 수립 : 가설 검정의 목적 확인, 귀무가설과 대립가설 설정, 유의수준(α) 결정
- 2. 가설 검정 수행 : 적절한 검정 통계량 결정, 검정 통계량과 p-value 계산
- 3. 검정 결과 판단 : p-value와 α를 비교
- p-value < α : 귀무가설 기각 => 대립가설 선택
- p-value > α : 귀무가설을 기각할 수 없음
가설
- 귀무가설(H0)
- 기존의 사실에 대한 가설, 검정의 대상이 되는 가설
- 검정통계량은 귀무가설의 분포에서 나옴
- 대립가설(H1)
- 새롭게 확인하고자 하는 사실에 대한 가설
- p-value가 작을 경우에 대립가설을 선택함(=검정통계량이 귀무가설에서 나온 것으로 보기 어려운 경우)
- 유의 확률(p-value)
- 귀무가설이 참이라는 가정하에 표본데이터가 귀무가설을 지지하는 확률
- p-value가 작을 수록 귀무가설이 틀렸다고 할 가능성이 커짐
- 최대허용한계보다 작은 경우(허용 한계보다 작으니 기존 한계를 설명할 수 없음) 현재 가설인 귀무가설을 기각해야 함


- 유의수준(α)
- 귀무가설을 기각하는 결정이 잘못될 수 있을 최대 가능성(최대 허용 한계) => 귀무가설이 실제로 참임에도 기각할 확률
- 단측 검정 : 한쪽만에 사용, 새로운 가설에 대해 판단 오류를 얼마나 위험을 tight하게 기준을 가질 것인가
- 양측 검정 : 양 쪽 끝에 존재 => α/2를 양쪽에서 사용
- 임계값
- 주어진 유의수준에서 귀무가설의 채택과 기각에 관련된 의사결정에서 기준이 되는 통계량
- 임계값 중심으로 귀무가설의 기각 영역과 채택 영역이 결정됨
가설 검정의 오류
- 제 1종 오류 : 귀무가설을 채택해야 함에도 불구하고 기각할 확률(=α)
- 제 2종 오류 : 귀무가설을 기각해야 함에도 불구하고 이를 채택할 확률(=β)

 참고
참고
평균 검정 : t-test
- 모집단에서 추출된 표본의 통계량을 이용하여 모집단의 평균의 차이에 대한 검정
- 모집단의 표준편차를 아는 경우, Z test를 사용함
- 두 집단의 평균 차이가 유의한지 검정하는 기법
- 평균의 차이가 표본 오차에 의한 것인지(귀무가설 채택) / 두 집단의 속성에 의한 것인지(귀무가설 기각)
- 독립성을 만족하지 않는 경우 : Paired t test
- 독립성은 만족하나 정규성을 만족하지 않는 경우 : Mann-Whitney test
- 독립성, 정규성은 있으나 등분산성이 없는 경우 : 2 sample t test
- 독립성, 정규성 그리고 등분산성을 만족하는 경우 : 독립 표본 T test
단일 표본 검정 : 1 sample t-test
- 단일 집단에 대한 모평균의 검정
- 단일 집단의 평균이 기존에 주장하는 평균과 다른지에 대한 검정
- ex) 공정 온도가 70도인데 다른 연구자들은 70도보다 높다고 한다면 어떤 가설이 맞는가

독립 2표본 검정 : 2 sample t-test
- 두 집단에 대한 평균 차이 검정 => 두 집단이 같은지 다른지를 확인함
- ex) 두 공급자 A와 B에 대해 두 공급자 간에 모평균에 차이가 있는가
- 두 확률 표본은 두 모집단으로부터 각기 독립적으로 관측되었을 때 사용 => 정규성은 맞지만 등분산성이 없는 경우
- 분석 절차
- 1. 정규성 검정 : A.D normality test => 양 끝에도 데이터 꽤 있는 경우(주로 사용함)
- 2. 등분산성 검정 : 두 집단을 검정하기 때문에 두 집단 간의 분산이 동일한지 검정
- 3. 평균 검정 방법 : Student's T Test(두 집단이 등분산인 경우) / Welch's T Test(두 집단의 분산이 다른 경우)
# 정규성 검정
from scipy.stats import shapiro
# 등분산성 검정(정규성 O)
from scipy.stats import bartlett
# 등분산성 검정(정규성 X)
from scipy.stats import levene
- 귀무가설 : 두 집단의 평균이 동일함 / 대립가설 : 두 집단의 평균은 다름


paired t-test
- 앞/뒤, 전/후 간의 비교를 하여 차이가 있는지 검정
- paired t-test는 하나의 단위의 차이를 검정함 => 짝을 이루는 집단의 평균 차이 검정
- 2 sample t-test : 집단 간의 차이를 검정
- 귀무가설 : 전 후의 평균 차이가 없음
- ex) 회사원 10명의 영어 성적이 학원가기 전과 후에 차이가 있는가

평균 검정 예제
- 모집단 표준편차를 아는 경우
- 현재까지 서비스 만족도가 7, 표준편차가 1.5, 최근 20명 조사, 표본평균이 6.0이 나옴
- H0 : 서비스 만족도가 7 / H1 : 서비스 만족도가 7이 아님
- Z = -2.976
Proportion test
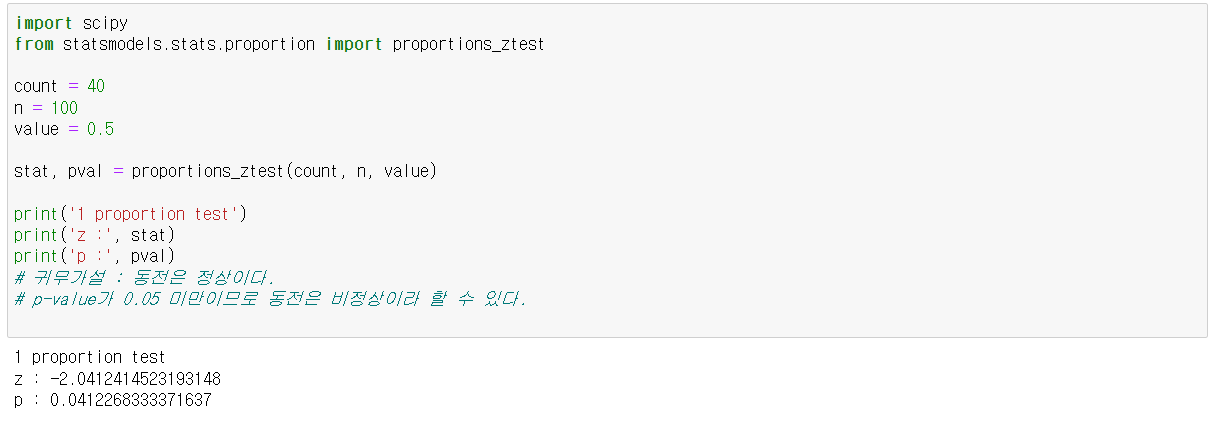
1 Proportion test
- 한 집단의 비율이 특정 비율과 같은지 검증하는 도구
- 귀무가설 : 모집단 비율(p)이 귀무가설에서의 비율(p0)과 같음
- ex) 정상적인 동전은 앞면이 나올 확률이 50%, 정상인지 검정하기 위해 100번 던져 앞면이 40번 나왔을 경우 동전은 정상인가?
2 Proportion test
- 두 집단의 비율이 같은지 검증하는 도구
- ex) 동일 제품을 생산하는 두 공장에서 A공장에서 1200개를 생산하여 14개의 불량품이 나왔고 B공장에서 1200개 중에서 5개의 불량품이 나온 경우 두 공정의 불량률이 같은가?

카이제곱 검정
- 관찰된 빈도가 기대되는 빈도와 의미있게 다른지 여부를 검증하는 방법
- 자료가 빈도로 주어진 경우, 특히 범주형 자료의 분석에 이용됨
- 교차표 상에서 행과 열이 독립적인지 판단 =>
- 관측 빈도 = 실제 수준, 기대 빈도 = 특정 분류 / 전체

- 검정 종류
- 동일성 검정 : 특성 별 두 가지 이상으로 분류된 범주 간에 상호 동일한 비율로 나타나는가를 검정
- 독립성 검정 : 특성 별 두 가지 이상으로 분류된 범주 간에 상호 관련성이 있는지 검정
- 적합도 검정 : 어떤 특성치 또는 사건이 기대치(또는 이론치)에 따라 발생했는지 여부를 검정
- 카이제곱 검정통계량이 크다 = 실측치 대비 기대치의 차이가 크다는 것을 의미 => 귀무가설 기각
- ex) 6가지 노트북 제품에 대해 7가지 제품 이미지 설문조사에서 각 제품에 대해 이미지에 대해 차이가 있는가

분산분석 : ANOVA
- 비교대상이 되는 집단들 간의 평균의 차이를 검증하기 위해 총 변동을 요인의 수준차이로 설명되는 변동과 설명될 수 없는 변동으로 분해하여 이 두 변동의 비가 통계적으로 유의한지 검정하는 분석 방법
- 3개 이상의 표본 평균을 동시에 비교하는 분석기법
- 기본 가정 : 독립성, 정규성, 등분산성 만족
- 귀무가설 : 각 집단의 수준별 평균 차이는 없음(군별 차이는 있지만 우연적)
- 총 변동을 2개의 변동으로 분리할 수 있음 => 오차에 의한 것, 수준에 의한 것
- 총 변동 = 오차에 의한 변동(각 수준 내에서의 변동) + 수준차에 의한 변동(수준 간의 변동)

- ex) 철강의 청정도를 높이기 위한 정련에서 강종별과 type에 따라 정련 시간의 차이가 있는가


상관분석
- 두 수량형 변수간에 선형적 관계의 강도와 방향을 분석하는 방법
- 산점도를 이용
- 두 변수 간의 연관된 정도를 나타낼 뿐, 인과관계를 설명하는 것은 아님
- 공분산 : 둘 이상의 변량이 연관성을 가지며 분포하는 모양을 전체적으로 나타낸 분산
- 한 변수의 변화가 다른 변수의 동등한 변화에 의해 왕복되는 한 쌍의 확률 변수 사이의 체계적인 관계
- 두 변수가 동일한 방향으로 움직일 때 : 공분산은 양의 큰 값
- 두 변수가 반대 방향으로 움직일 때 : 공분산은 음의 큰 값
- -∞ 에서 +∞ 사이의 값을 가짐
- 척도의 단위에 따라 달라짐
- 상관계수 : 두 변수 간의 선형적인 관계 정도와 방향을 수치로 표시한 지수
- 두 개 이상의 임의 변수가 나란히 움직이는 정도를 결정하는 통계의 척도
- 단위에 영향을 받지 않음
- -1부터 1 사이의 값을 가짐


































