예측모델 - 주성분 분석/시계열 분석

주성분 분석

주성분 분석

• 정의 : 변수 간의 관계(공분산, 상관)를 기반으로 정보 손실을 최소화하면서 주요 성분을 확인하고 차원을 축소하는 기법
  • 차원 : 많은 변수를 줄여 변수를 적게 만드는 것에 사용됨
• 주성분 : 변수 간의 선형 결합으로 특징을 반영하는 주성분 선택
• 주성분 분석 주의사항
  • 변수 scale이 유사해야함 => scaling이 필요
    • scale이 유사하면 공분산 행렬, scale 차이가 크면 상관계수를 이용
    • 공분산 : 각 확률변수들이 어떻게 퍼져있는지를 나타내는 것
    • 상관계수 : 확률변수의 절대적 크기에 영향을 받지 않도록 단위화
  • 주성분 점수 : 고유치 및 고유벡터를 계산해 고유 벡터의 계수를 이용해 계산한 결과

• 활용 용도
  • 변수 Screening : 변수가 많은 경우 주요 특징을 보이는 주성분 선택을 통한 변수 축소
  • 특징을 반영한 지표(변수 간의 선형 결합) 생성 => 모니터링 및 이상 탐지
  • 다른 분석 기법의 사전 단계로 활용

주성분

• 주성분 고유벡터 : 주성분은 입력변수의 선형관계
  • 고유벡터 : 선형변환 A에 의한 변환 결과가 자기 자신의 상수배가 되는 0이 아닌 벡터

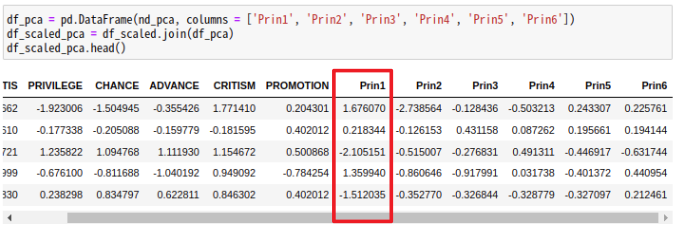
• 주성분 기여율 : 입력 변수의 총변동을 생성된 개별 주성분이 설명하는 변동의 크기로 내림차순으로 표시
  • 기여율 = 주성분의 고유값 / 주성분 고유값 전체
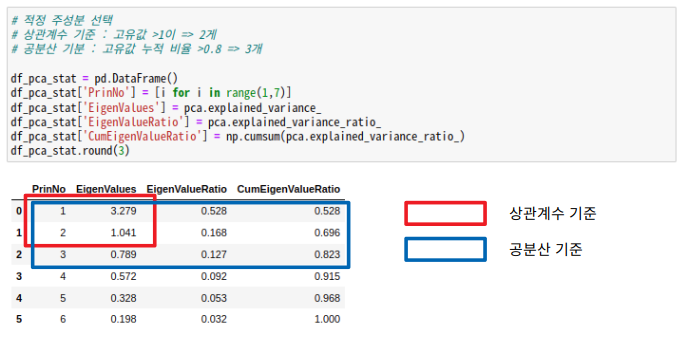
• 주성분 개수 결정
  • 1. 상관계수 행렬 사용시 : 고유값 ≥ 1
  • 2. 공분산 행렬 사용시 : 고유값 누적 비율 ≥ 80~85% ( 정보 손실을 20% 미만으로 유지) => 주로 사용 
    • 공분산 : 2개 변수가 함께 변하는 정도(joint variability)의 척도
  • 3. Scree Plot 이용 : 고유치(Y) * 주성분순차 번호 산점도
    • elbow : 고유치가 감소 경향을 시각적으로 표현한 것으로 급격히 감소하는 지점에서 개수 결정

주성분 해석

• 주성분 고유 벡터 : 주성분에 대한 입력변수의 선형 계수로 방향과 크기 검토
  • 음수인지 양수인지로 방향성을,  선형 계수 값으로 크기를 검토함
• 주성분 명칭 부여 : 고유벡터의 방향과 크기를 기준으로 유사 패턴의 입력변수 그룹형성
• 주성분 활용 : 주성분을 지표화하여 관리 효율 향상
• 주성분 성질 : 주성분의 변동 합은 고유치 합과 같음, 설명하는 변동의 크기는 상호 독립적

 

• Raw_data에서 PCA를 수행하기 위한 n_components는 기존 데이터의 설명변수의 갯수이다.

 

PCA 순서(간략)

 

• 데이터를 불러와서 목표변수와 설명변수 분리
• sns.pairplot으로 변수별 분포를 파악하고 corr를 통해 상관관계 보이기
• 분포가 다르므로 Scaling

• 주성분 분석

• 고유값(EigenValue) 확인 및 주성분 개수 설정 => 공분산 행렬 / 상관계수 행렬

• Scree Plot 확인 및 주성분 개수 설정

• 고유값과 누적 고유값 확인하기

 

 

시계열 분석

Time Series

• 정의 : 시계열 데이터를 분해하여 생성한 수학적 모델을 활용하여 미래의 값을 예측하는 분석 기법
• 시계열 데이터 : 시간의 흐름에 따라 수집된 데이터

 

 

 

ㅇ