데이터의 양이 많은 경우 한눈에 데이터의 분포를 알기 힘들다. 그렇기에 다양한 함수를 통해 데이터의 분포를 한눈에 알 수 있다. 아래에서 다양한 데이터 분포 탐색 방법에 대해 알아보고자 한다. 마지막으로 데이터 분포의 변이에 대해 살펴볼 것이다. 데이터가 평균값와 떨어진 정도를 나타내는 분산, 표준편차에 대해 알아보고 정규 분포에 대해 알아보겠다.
1. 백분위수와 사분위수
사분위수란 자료를 크기 순으로 배열하고, 누적 백분율을 4 등분한 각 점에 해당하는 값을 말한다. 제1사분위수는 누적 백분율이 25%에 해당하는 점, 제2사분위수는 누적 백분율이 50%에 해당하는 점, 제3사분위수는 75%, 제4사분위수는 100%에 해당하는 점수이다. 사분위수는 quantile() 함수를 사용하여 구할 수 있다.
A_salary <- c(25,28,50,60,30,35,40,70,40,70,40,100,30,30)
B_salary <- c(20,40,25,25,35,25,20,10,55,65,100,100,150,300)
quantile(A_salary, 0.9) # 90% 백분위수
quantile(B_salary, 0.9)
quantile(A_salary) # 사분위수
'''
0% 25% 50% 75% 100%
25.0 30.0 40.0 57.5 100.0
'''
quantile(B_salary) '''
0% 25% 50% 75% 100%
10.00 25.00 37.50 91.25 300.00
'''quantile() 함수에 소수점을 부여하여 백분위수를 구할 수 있고 quantile()에 값을 가진 매개변수만을 넣는 경우 사분위수를 알 수 있다.
2. 상자 그림(상자수염그림)
boxplot() 함수로 상자 그림을 통해 데이터셋의 범위, 사분위수, 중앙값 등을 알 수 있다.
A_salary <- c(25,28,50,60,30,35,40,70,40,70,40,100,30,30)
B_salary <- c(20,40,25,25,35,25,20,10,55,65,100,100,150,300)
boxplot(A_salary, B_salary, names=c('A 회사 Salary', 'B 회사 Salary'))
위의 <그림1>에서 B회사의 Salary 상자그림에 보면 위에 동그라미 하나가 생김을 확인할 수 있다. 이는 이상값으로 상자그림을 통해 데이터의 분포를 파악하고 이질적인 값을 가진 데이터를 파악할 수 있다.
3. 히스토그램
히스토그램은 hist() 함수를 이용해 연속형 수치 데이터의 경우 분포의 시각화에 사용된다. 히스토그램은 앞서 말했듯이 연속형 수치 데이터에 사용되는데 이와 비교해 볼수 있는 막대그래프의 경우 이산형 수치 데이터나 범주형 데이터에 사용된다. 두 그래프에는 차이가 있는데 히스토그램의 경우 막대간 간격이 없는 반면, 막대 그래프의 경우 막대간 간격이 존재한다.
A_salary <- c(25,28,50,60,30,35,40,70,40,70,40,100,30,30)
B_salary <- c(20,40,25,25,35,25,20,10,55,65,100,100,150,300)
hist(A_salary, xlab='A사 Salary', ylab='인원수', breaks =5)
hist(B_salary, xlab='B사 Salary', ylab = '인원수', breaks = 5)
# xlab : x축 레이블명 지정
# ylab : y축 레이블명 지정
# breaks : 매개인자의 숫자만큼 구간을 나누어 배치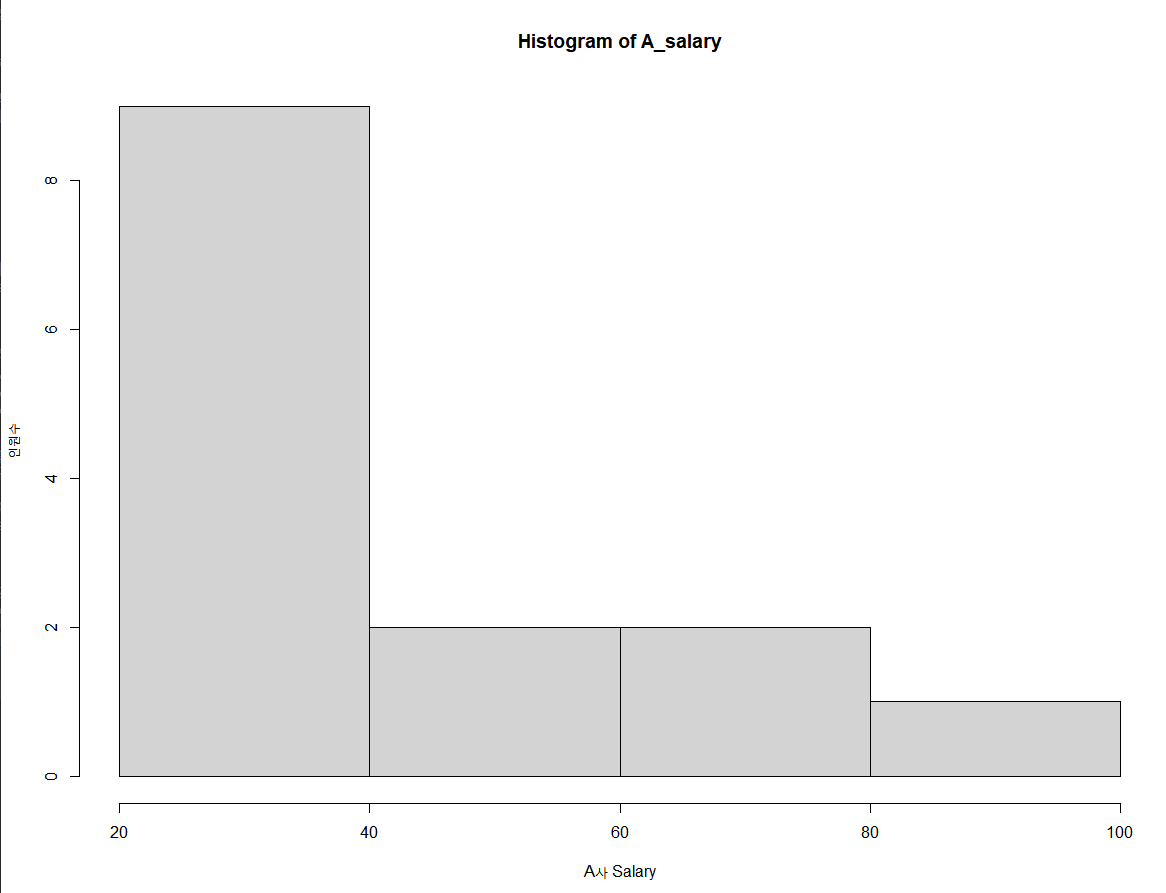 |
 |
<그림2>
4. 도수 분포표
도수분포표는 히스토그램을 시각화한 것이다. 수집된 데이터를 동일한 크기의 구간으로 분류하고 각 구간마다 데이터의 개수를 정리한 표이다. 수치형 데이터와 범주형 데이터에 따라 사용되는 함수가 다른데 수치형의 경우 cut() 함수를, 범주형의 경우 table() 함수를 사용하여 도수분포표를 작성한다.
# 수치형 데이터 : cut() 함수
A_salary <- c(25,28,50,60,30,35,40,70,40,70,40,100,30,30)
cut_value1 <- cut(A_salary, breaks = 5) # 데이터 구간을 5개로 나누어 도수분포표 생성
freq1 <- table(cut_value1)
freq1
'''
cut_value1
(24.9,40] (40,55] (55,70] (70,85] (85,100]
9 1 3 0 1 '''
B_salary <- c(20,40,25,25,35,25,20,10,55,65,100,100,150,300)
cut_value2 <- cut(B_salary, breaks = 5)
freq2 <- table(cut_value2)
freq2
'''
cut_value2
(9.71,68] (68,126] (126,184] (184,242] (242,300]
10 2 1 0 1 '''
# 범주형 데이터 : table() 함수
A_gender <- as.factor(c('남','남','남','남','남','남','남','남','남','여','여','여','여','여'))
B_gender <- as.factor(c('남','남','남','남','여','여','여','여','여','여','여','남','여','여'))
A <- data.frame(gender <- A_gender, salary <- A_salary)
B <- data.frame(gender <- B_gender, salary <- B_salary)
freqA <- table(A$gender)
freqA
'''
남 여
9 5 '''
freqB <- table(B$gender)
freqB
'''
남 여
5 9 '''
# 범주가 어느 정도 비중을 차지하는지 알아보기(빈도표) : prop.table
prop.table(freqA)
'''
남 여
0.6428571 0.3571429 '''
prop.table(freqB)
'''
남 여
0.3571429 0.6428571 '''
5. 막대 그래프
위에서 언급했듯이 범주형 데이터나 이산형 수치 데이터의 도수분포표를 시각화 하는 그래프이다. 막대 그래프에는 barplot() 함수가 사용된다.
barplot(freqA, names=c('남','녀'), col = c('skyblue','pink'), ylim =c(0,10), main = 'A사')
# names : 막대 이름, col : 색상, ylim : y축 범위, main : plot의 제목
barplot(freqB, names = c('남','여'), col = c('blue','red'), ylim = c(0,10))
title(main ='B사',xlab='구분', ylab='수')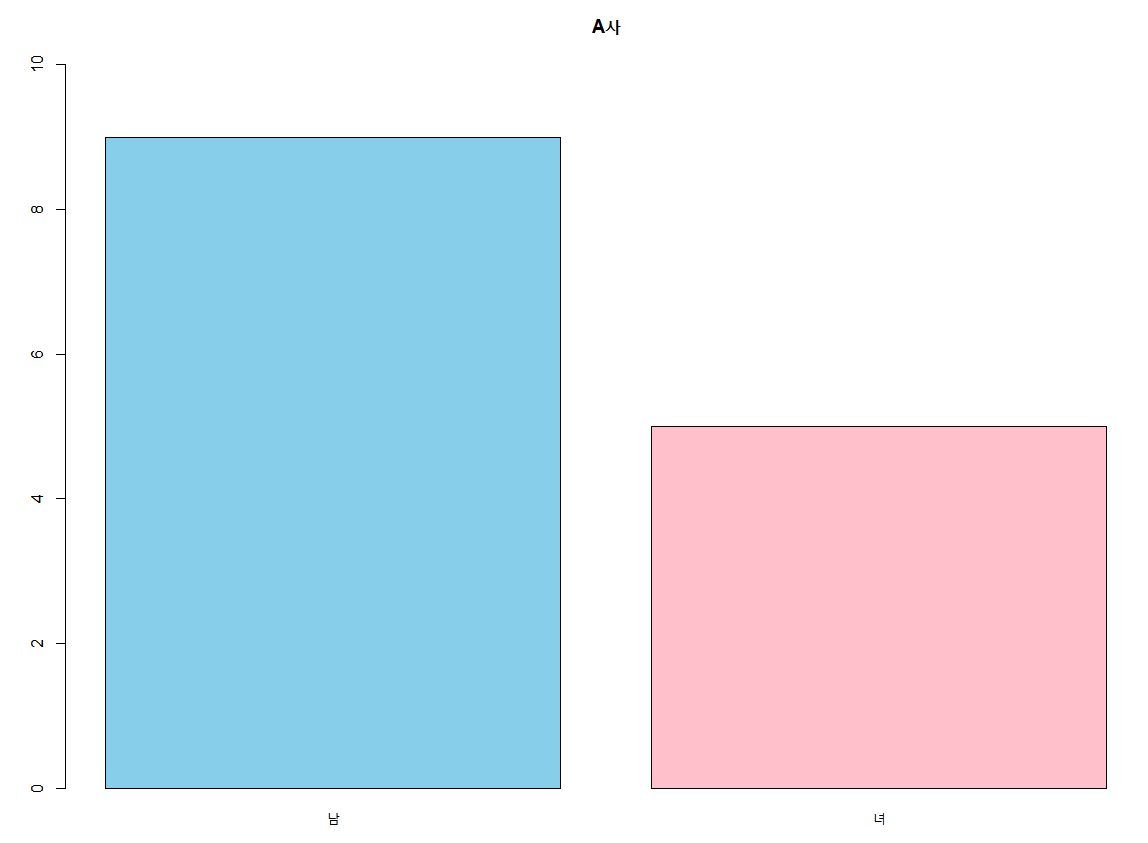 |
 |
<그림3>
6. 파이 그래프
pie() 함수를 통해 데이터의 분포를 원의 형태로 나타낸 그래프이다.
범주가 많거나 크기의 차이가 근소한 경우 사용하지 않는다. 이 경우 대개 막대 그래프를 활용한다.
pie(x=freqA, c('남','여'), main = 'A사')
pie(x=freqB, labels = c('남','여'),radius=1, clockwise=T)
# clockwise : 시계 방향으로 데이터 분포 시각화 |
 |
<그림4>
< 데이터 분포 변이 >
1. 분산과 표준편차
데이터 분포 변이를 살펴보기 위해 데이터의 평균값을 알아야 한다. 평균값에 대해 얼마나 멀리 떨어져 있는가를 나타내는 두 지표가 있는데 이는 분산과 표준편차이다. 분산이란 평균으로부터 떨어져있는 각 데이터 사이의 거리를 제곱한 평균이고 표준편차는 데이터가 평균값으로부터 얼마나 떨어져있는가를 측정한 것이다.
x <- c(63,43,45,37,28,28,46,70,25,5,48,62,43,27,16)
var(x)
'''
[1] 323.9238 '''
sd(x)
'''
[1] 17.99788 '''아래 코드는 sales_result.csv 데이터로 표준편차와 분산을 살펴 보았다.
data <- read.csv("sales_result.csv", sep=',', header = T)
head(data, 5)
'''
월별 AI드럼세탁기 둥글청소기
1 13-Jan 8530 6830
2 13-Feb 7045 9464
3 13-Mar 7316 6809
4 13-Apr 7162 6417
5 13-May 6843 7469 '''
summary(data)
'''
월별 AI드럼세탁기 둥글청소기
Length:24 Min. :6101 Min. :4900
Class :character 1st Qu.:6804 1st Qu.:5750
Mode :character Median :7000 Median :6994
Mean :6986 Mean :6994
3rd Qu.:7172 3rd Qu.:7840
Max. :8530 Max. :9464 '''
var(data$AI드럼세탁기)
'''
[1] 288519.9 '''
sd(data$AI드럼세탁기)
'''
[1] 537.1405 '''
※ 참고
위의 데이터로 앞서 살펴본 boxplot에 대해 실습해 보도록 하겠다
boxplot(data$AI드럼세탁기, data$둥글청소기,
names = c('AI드럼', '둥글'), col =c('red','blue'), main='판매실적비교')
'R' 카테고리의 다른 글
| 상관 분석 (0) | 2021.07.27 |
|---|---|
| 추론통계(귀무가설과 대립가설, 유의 확률, t-검정, 분산분석) (0) | 2021.07.27 |
| dplyr 패키지(select, distinct, arrange, group_by, filter, summarise, mutate) (0) | 2021.07.26 |
| 빈도 분석 실습(지역 별 교통사고 사건 데이터) (0) | 2021.07.25 |
| 변수간 관계 탐색(산점도, pairs, 상관계수, 상관행렬, 상관행렬 히트맵) (0) | 2021.07.25 |

